Persamaan Kutub dan Grafiknya

Sistem koordinat kutub memberikan alternatif pilihan di samping sistem koordinat kartesius. Ada kurva-kurva yang persamaannya sederhana dalam suatu sistem dan ada kurva yang persamaannya sederhana dalam sistem lain. Banyak kurva yang rumit, namun  persamaannya sederhana apabila dinyatakan dengan koordinat kutub. Demikian pula dalam perhitungan-perhitungan, kadang-kadang dengan menyatakan persamaannya dengan koordinat kutub, perhitungan akan menjadi lebih sederhana.

Berikut ini bentuk baku persamaan kutub dari beberapa kurva

θ = θ₀      persamaan garis lurus melalui kutub dan membentuk sudut θ₀ dengan sumbu kutub

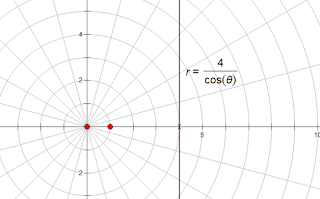
persamaan garis lurus yang berjarak d satuan dari kutub dan normalnya membentuk sudut θ₀ dengan sumbu kutub

persamaan garis lurus yang tegak lurus sumbu kutb dan melalui titik (d,0)

persamaan garis lurus yang sejajar sumbu kutub dan melalui titik (d, π/2)

persamaan lingkaran yang berpusat di (a , θ₀) dan berjari-jari a

persamaan lingkaran yang berpusat di (a,0) dan berjari-jari a

persamaan lingkaran yang berpusat di (a,π/2) dan berjari-jari a

persamaan lingkaran yang berpusat di kutub dan berjari-jari a

persamaan konik dengan fokus di kutub dan garis arah berjarak d dari kutub serta normalnya membentuk sudut θ₀ dengan sumbu kutub dan keeksentrikan e

persamaan konik dengan fokus di kutub dan garis arah tegak lurus pada sumbu kutub sejauh d satuan dari kutub.

persamaan konik dengan fokus di kutub dan garis arah sejajar sumbu kutub sejauh d satuan dari kutub.

dengan a dan b konstanta positik menyatakan persamaan limason

menyatakan persamaan kardioda.

grafiknya disebut lemniskat dan berbentuk seperti angka delapan

grafiknya dinamakan mawar. Banyaknya daun mawar adalah n jika n ganjil dan 2n jika n genap.

disebut persamaan spiral archimedes.

disebut persamaan spiral archimedes.